TP5 : Neural Tangent Kernel

import torch

import torch.optim as optim
import torch.nn as nn
import torch.nn.functional as F

from torchvision import datasets, transforms
import torchvision

import numpy as np
import matplotlib.pyplot as plt

from IPython.display import clear_output

clear_output()

Today we study attempt to compare the behavior of neural nets and their NTK on some simple example.

The data

To do so we are going to use the FashionMNIST dataset to build a small binary classification task, train some neural nets on those tasks, and build the corresponding NTK.

n = 200  # number of training points that we keep
c1, c2 = 1, 3  # subclasses that are kept, make sure that c1 < c2

batch_size = 32  # training batch size

classes = (
    "T-shirt/Top",
    "Trouser",
    "Pullover",
    "Dress",
    "Coat",
    "Sandal",
    "Shirt",
    "Sneaker",
    "Bag",
    "Ankle Boot",
)

# Define a sequence of operations that will be performed to all training images before use
# the 'ToTensor()' function sets the image in tensor object and puts the values of every pixel between 0 and 1
# the 'Normalize' performs the dataset to a given mean and variance
transform = transforms.Compose(
    [transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,))]
)

# Creates an object to load the images. We use FashionMNIST as a substitute for MNIST because binary classification on
# subclasses of MNIST is too easy.

trainset = datasets.FashionMNIST(
    "../data", train=True, download=True, transform=transform
)

r = torch.arange(len(trainset))

# Build a training set that only contains images with classes c1 and c2, with n / 2 images from each label.

idxc1 = torch.as_tensor(trainset.targets) == c1
x1 = np.where(np.cumsum(idxc1) == (n / 2))[0][0]
idxc1 = idxc1 & (r <= x1)

idxc2 = torch.as_tensor(trainset.targets) == c2
x2 = np.where(np.cumsum(idxc2) == (n / 2))[0][0]
idxc2 = (torch.as_tensor(trainset.targets) == c2) & (r <= x2)

idx = idxc1 + idxc2
dset_train = torch.utils.data.dataset.Subset(trainset, np.where(idx == 1)[0])

print(f"Number of training points : {len(dset_train)}")
trainloader = torch.utils.data.DataLoader(dset_train, batch_size=batch_size)

# Build the corresponding test set

testset = datasets.FashionMNIST(
    root="./data", train=False, download=True, transform=transform
)
clear_output()
idx = torch.as_tensor(testset.targets) == c1
idx += torch.as_tensor(testset.targets) == c2
dset_test = torch.utils.data.dataset.Subset(testset, np.where(idx == 1)[0])
testloader = torch.utils.data.DataLoader(dset_test)

def imshow(img):
    img = img / 2 + 0.5  # unnormalize
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
    plt.show()


# get batch_size random training images
dataiter = iter(trainloader)
images, labels = next(dataiter)

# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(" ".join(f"{classes[labels[j]]:5s}" for j in range(batch_size)))

Dress Trouser Dress Trouser Dress Dress Trouser Dress Dress Dress Dress Dress Dress Trouser Dress Trouser Dress Trouser Trouser Trouser Dress Trouser Dress Dress Trouser Trouser Trouser Trouser Trouser Dress Trouser Trouser

A neural network

Fully connected 1-hidden layer neural network. Flattens the image and treats it as a vector.

Use the methods

nn.Flatten nn.Linear

nn.init.xavier_normal_ nn.init.zeros_

to build the network

class MLPshallow(nn.Module):
    def __init__(self, hidden_dim=10):
        super().__init__()
        self.hidden_dim = hidden_dim
        self.flatten = nn.Flatten()
        self.l1 = nn.Linear(28 * 28, self.hidden_dim)
        self.lout = nn.Linear(self.hidden_dim, 1)

        nn.init.xavier_normal_(self.l1.weight)
        nn.init.xavier_normal_(self.lout.weight)

        nn.init.zeros_(self.l1.bias)
        nn.init.zeros_(self.lout.bias)

    def forward(self, x):
        x = self.flatten(x)
        x = F.relu(self.l1(x))
        x = self.lout(x)
        return x


net = MLPshallow(hidden_dim=2000)

class MLPshallow(nn.Module):
    def __init__(self, hidden_dim=10):
        super().__init__()
        self.hidden_dim = hidden_dim
        # YOUR CODE HERE

    def forward(self, x):
        # YOUR CODE HERE
        return x


net = MLPshallow(hidden_dim=1000)

The training function

We train the network with the square loss to predict the class. The labels are normalized to be between \(0\) and \(1\).

i.e. the y-value for images with label i is float(i/9)

Write the training function.

def train(net, trainloader, N_passes=1, lr=0.01):
    optimizer = optim.SGD(net.parameters(), lr=lr)
    criterion = nn.MSELoss()

    losses = []
    i = 0

    for _ in range(N_passes):
        for inputs, labels in trainloader:
            i += 1
            optimizer.zero_grad()

            # print(inputs.shape)
            # print(torch.linalg.vector_norm(inputs, dim=(1, 2, 3)))

            outputs = net(inputs)
            target = labels.float().unsqueeze(1) / 9
            loss = criterion(outputs, target)

            loss.backward()
            optimizer.step()

            losses.append(loss.detach().numpy())

    print(f"Number of gradient steps {i}")

    return losses

def train(net, trainloader, N_passes=1, lr=0.01):
    optimizer = optim.SGD(net.parameters(), lr=lr)
    criterion = nn.MSELoss()

    losses = []
    i = 0

    for _ in range(N_passes):
        for inputs, labels in trainloader:
            i += 1

            # YOUR CODE HERE

            losses.append(loss.detach().numpy())

    print(f"Number of gradient steps {i}")

    return losses

print("Batch size : ", batch_size)

losses = train(net, trainloader, N_passes=200, lr=0.01)

plt.ylim(0, 1.1 * np.max(losses))
plt.plot(losses)
plt.grid(alpha=0.3)

Batch size :  32
Number of gradient steps 1400

Checking the training values

Complete the following function to get the prediction of the network on the data.

Train the network until you interpolate the data.

correct = 0
total = 0
with torch.no_grad():
    for images, labels in trainloader:
        outputs = net(images)
        predicted = c1 + (c2 - c1) * (
            9 * outputs > (c1 + c2) / 2
        )  # c1 if prediction is less than average,

        total += labels.size(0)
        correct += (predicted.squeeze(1) == labels).sum()

print(
    f"Accuracy of the network on the {total} train images: {100 * correct // total} %"
)

Accuracy of the network on the 200 train images: 100 %

correct = 0
total = 0
with torch.no_grad():
    for images, labels in trainloader:

        outputs = net(images)
        predicted = #YOUR CODE HERE

        total += labels.size(0)
        correct += (predicted.squeeze(1) == labels).sum()

print(f'Accuracy of the network on the {total} train images: {100 * correct // total} %')

testloader = torch.utils.data.DataLoader(dset_test, batch_size=64)
dataiter = iter(testloader)
images, labels = next(dataiter)

# print images
imshow(torchvision.utils.make_grid(images[32:40]))
print("GrndTruth: ", " ".join(f"{classes[labels[j]]:5s}" for j in range(8)))

with torch.no_grad():
    outputs = net(images)
    predicted = c1 + (c2 - c1) * (9 * outputs > (c1 + c2) / 2)

    print("Predicted: ", " ".join(f"{classes[predicted[j]]:5s}" for j in range(8)))

GrndTruth:  Trouser Trouser Trouser Dress Trouser Trouser Dress Dress
Predicted:  Trouser Trouser Trouser Dress Trouser Trouser Dress Dress

testloader = torch.utils.data.DataLoader(dset_test, batch_size=8)
dataiter = iter(testloader)
images, labels = next(dataiter)

# print images
imshow(torchvision.utils.make_grid(images[:8]))
print('GrndTruth: ', ' '.join(f'{classes[labels[j]]:5s}' for j in range(8)))

with torch.no_grad():
    outputs = net(images)
    predicted = #YOUR CODE HERE

    print('Predicted: ', ' '.join(f'{classes[predicted[j]]:5s}' for j in range(8)))

  Cell In[17], line 11
    predicted = #YOUR CODE HERE
                ^
SyntaxError: invalid syntax

Test loss

correct = 0
total = 0
with torch.no_grad():
    for images, labels in testloader:
        outputs = net(images)
        predicted = c1 + (c2 - c1) * (
            9 * outputs > (c1 + c2) / 2
        )  # c1 if prediction is less than average,

        total += labels.size(0)
        correct += (predicted.squeeze(1) == labels).sum()

print(f"Accuracy of the network on the {total} test images: {100 * correct // total} %")

Accuracy of the network on the 2000 test images: 92 %

correct = 0
total = 0
with torch.no_grad():
    for images, labels in testloader:
        outputs = net(images)
        predicted = #YOUR CODE HERE

        total += labels.size(0)
        correct += (predicted.squeeze(1) == labels).sum()

print(f'Accuracy of the network on the {total} test images: {100 * correct // total} %')

The NTK

Let us write the corresponding NTK in the infinite width limit. Use the formula seen in class for the NTK kernel to complete the code below.

class NTK:
    def __init__(self, dset_train):
        self.n = len(dset_train)
        self.train_set = dset_train
        self.train()

    def k(self, x, xprime):
        """
        NTK Kernel for ReLU with one hidden layer. The delta factor
        is to avoid nan values for arccos(1+eps) from rounding.
        """
        with torch.no_grad():
            v = torch.linalg.norm(x) * torch.linalg.norm(xprime)
            u = 0.99999 * torch.dot(x, xprime) / v
            return v * (
                u * (torch.pi - torch.arccos(u) + torch.sqrt(1 - u**2)) / (2 * np.pi)
                + u * (torch.pi - torch.arccos(u)) / (2 * np.pi)
            )

    def train(self):
        ntrainloader = torch.utils.data.DataLoader(self.train_set, batch_size=self.n)
        dataiter = iter(ntrainloader)
        images, labels = next(dataiter)
        print(images.flatten(start_dim=1, end_dim=3).shape)

        xis = images.flatten(start_dim=1, end_dim=3)
        print(xis.shape)

        self.xis = xis

        # plt.imshow(xis)
        # plt.title('Flattened images')
        # plt.show()

        H = torch.empty((n, n))

        for i in range(n):
            for j in range(n):
                H[i, j] = self.k(xis[i], xis[j])

        # plt.title(f'Gram matrix for {n} x {n} inputs')
        # plt.imshow(H)
        # plt.colorbar()
        # plt.show()

        eigenvalues = np.linalg.eigvalsh(H)
        print(f"Smallest eigenvalue : {eigenvalues[0]}")
        # plt.title('Sorted eigenvalues of the Gram matrix')
        # plt.plot(eigenvalues)
        # plt.grid(alpha=0.3)
        # plt.ylim(0, 1.01 * np.max(eigenvalues))
        # plt.show()

        self.H = H
        self.Hinv = torch.linalg.inv(H)
        self.V = self.Hinv @ labels.float() / 9

        print(self.V.shape)

        # plt.imshow(V)
        # plt.colorbar()
        # plt.show()

    def apply(self, x):
        s = 0
        for i, xi in enumerate(self.xis):
            s += self.k(x, xi) * self.V[i]  # V = ((Phi^\top Phi)^{-1} Y)
        return s

    def gen_bound(self):
        ntrainloader = torch.utils.data.DataLoader(self.train_set, batch_size=n)
        dataiter = iter(ntrainloader)
        _, labels = next(dataiter)

        return torch.dot(labels.float(), self.Hinv @ labels.float())

class NTK:
    def __init__(self, dset_train):
        self.n = len(dset_train)
        self.train_set = dset_train
        self.train()

    def k(self, x, xprime):
        """
        NTK Kernel for ReLU with one hidden layer. T
        """
        delta = 0.999999
        with torch.no_grad():
            v = torch.linalg.norm(x) * torch.linalg.norm(xprime)
            u = delta * torch.dot(x, xprime) / v
            return  # YOUR CODE HERE

    def train(self):
        ntrainloader = torch.utils.data.DataLoader(self.train_set, batch_size=self.n)
        dataiter = iter(ntrainloader)
        images, labels = next(dataiter)
        print(images.flatten(start_dim=1, end_dim=3).shape)

        xis = images.flatten(start_dim=1, end_dim=3)
        print(xis.shape)

        self.xis = xis

        # plt.imshow(xis)
        # plt.title('Flattened images')
        # plt.show()

        H = torch.empty((n, n))

        for i in range(n):
            for j in range(n):
                H[i, j] = self.k(xis[i], xis[j])

        # plt.title(f'Gram matrix for {n} x {n} inputs')
        # plt.imshow(H)
        # plt.colorbar()
        # plt.show()

        eigenvalues = np.linalg.eigvalsh(H)
        print(f"Smallest eigenvalue : {eigenvalues[0]}")
        # plt.title('Sorted eigenvalues of the Gram matrix')
        # plt.plot(eigenvalues)
        # plt.grid(alpha=0.3)
        # plt.ylim(0, 1.01 * np.max(eigenvalues))
        # plt.show()

        self.H = H
        self.Hinv = torch.linalg.inv(H)
        self.V = self.Hinv @ labels.float() / 9

        print(self.V.shape)

        # plt.imshow(V)
        # plt.colorbar()
        # plt.show()

    def apply(self, x):
        s = 0
        for i, xi in enumerate(self.xis):
            s += self.k(x, xi) * self.V[i]
        return s

ntk = NTK(dset_train)

torch.Size([200, 784])
torch.Size([200, 784])
Smallest eigenvalue : 13.815045356750488
torch.Size([200])

ntk_trainloader = torch.utils.data.DataLoader(dset_train, batch_size=1)

correct_ntk = 0
total = 0
with torch.no_grad():
    for images, labels in ntk_trainloader:
        x = torch.flatten(images.squeeze(0))

        output_ntk = ntk.apply(x)
        predicted_ntk = c1 + (c2 - c1) * (
            9 * output_ntk > (c1 + c2) / 2
        )  # c1 if prediction is less than average,
        correct_ntk += (predicted_ntk.unsqueeze(0) == labels).numpy()[0]

        total += 1

print(f"Accuracy of NTK on the {total} train images: {100 * correct_ntk // total} %")

Accuracy of NTK on the 200 train images: 100 %

Let us now compare the outputs of the NTK and of the network.

What do you observe? Why?

testloader = torch.utils.data.DataLoader(dset_test)

total = 0
correct_ntk = 0
correct_net = 0
agree = 0

with torch.no_grad():
    for images, labels in testloader:
        x = torch.flatten(images.squeeze(0))

        output_ntk = ntk.apply(x)
        predicted_ntk = c1 + (c2 - c1) * (
            9 * output_ntk > (c1 + c2) / 2
        )  # c1 if prediction is less than average,
        correct_ntk += (predicted_ntk.unsqueeze(0) == labels).numpy()[0]

        outputs = net(images)
        predicted = c1 + (c2 - c1) * (
            9 * outputs > (c1 + c2) / 2
        )  # c1 if prediction is less than average,
        correct_net += (predicted.squeeze(1) == labels).numpy()[0]

        # print(labels.shape)
        # print(predicted_ntk.unsqueeze(0).shape, predicted_ntk.unsqueeze(0))
        # print(predicted.squeeze(1).shape, predicted.squeeze(1))

        agree += (predicted_ntk.unsqueeze(0) == predicted.squeeze(1)).numpy()[0]
        total += 1

print(f"Accuracy of NTK on the {total} test images: {100 * correct_ntk // total} %")
print(f"Accuracy of net on the {total} test images: {100 * correct_net // total} %")

print(f"Both methods agree on {100 * agree // total} % of the images")

Accuracy of NTK on the 2000 test images: 96 %
Accuracy of net on the 2000 test images: 92 %
Both methods agree on 94 % of the images

Generalization error

trainset = datasets.FashionMNIST(
    "../data", train=True, download=True, transform=transform
)
r = torch.arange(len(trainset))

bounds = []

n_values = range(100, 2000, 300)

for n in n_values:
    # Build a training set that only contains images with classes c1 and c2, with n / 2 images from each label.

    idxc1 = torch.as_tensor(trainset.targets) == c1
    x1 = np.where(np.cumsum(idxc1) == (n / 2))[0][0]
    idxc1 = idxc1 & (r <= x1)

    idxc2 = torch.as_tensor(trainset.targets) == c2
    x2 = np.where(np.cumsum(idxc2) == (n / 2))[0][0]
    idxc2 = (torch.as_tensor(trainset.targets) == c2) & (r <= x2)

    idx = idxc1 + idxc2
    dset_train = torch.utils.data.dataset.Subset(trainset, np.where(idx == 1)[0])

    ntk = NTK(dset_train)
    bounds.append(ntk.gen_bound())

torch.Size([100, 784])
torch.Size([100, 784])
Smallest eigenvalue : 23.512008666992188
torch.Size([100])
torch.Size([400, 784])
torch.Size([400, 784])
Smallest eigenvalue : 15.195989608764648
torch.Size([400])
torch.Size([700, 784])
torch.Size([700, 784])
Smallest eigenvalue : 13.155244827270508
torch.Size([700])
torch.Size([1000, 784])
torch.Size([1000, 784])
Smallest eigenvalue : 5.420177936553955
torch.Size([1000])
torch.Size([1300, 784])
torch.Size([1300, 784])
Smallest eigenvalue : 5.3553948402404785
torch.Size([1300])
torch.Size([1600, 784])
torch.Size([1600, 784])
Smallest eigenvalue : 5.308578968048096
torch.Size([1600])
torch.Size([1900, 784])
torch.Size([1900, 784])
Smallest eigenvalue : 5.274092197418213
torch.Size([1900])

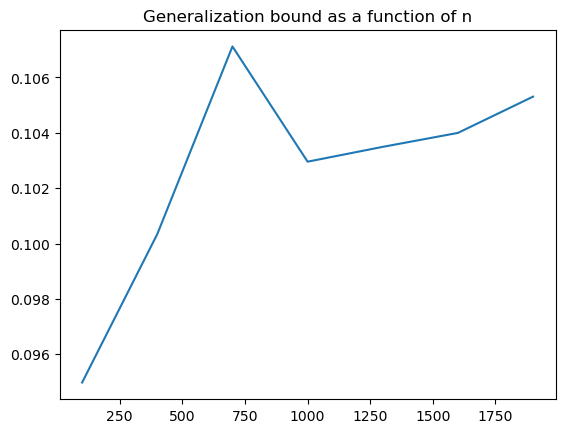
plt.title("Generalization bound as a function of n")
plt.plot(n_values, np.sqrt(bounds / np.array(n_values)))

[<matplotlib.lines.Line2D at 0x147f2fd30>]

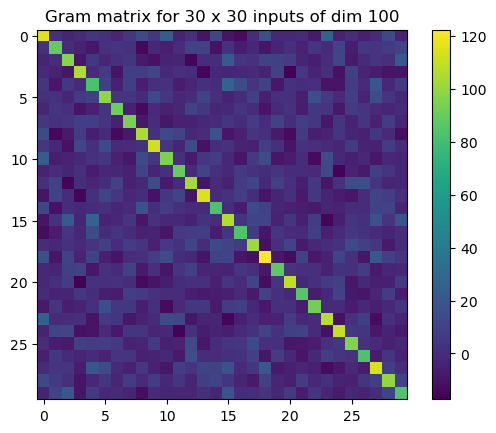
The NTK Gram matrix is typically invertible

if number of data points is smaller than input dim

n = 30
d = 100

xis = [torch.randn(d) for _ in range(n)]

# print(xis)
# print(np.dot(xis[n-1], xis[n-1]))

H = torch.empty((n, n))


def k(x, xprime):
    with torch.no_grad():
        v = torch.linalg.norm(x) * torch.linalg.norm(xprime)
        u = 0.99999 * torch.dot(x, xprime) / v
        return v * (
            u * (torch.pi - torch.arccos(u) + torch.sqrt(1 - u**2)) / (2 * np.pi)
            + u * (torch.pi - torch.arccos(u)) / (2 * np.pi)
        )


for i in range(n):
    for j in range(n):
        H[i, j] = k(xis[i], xis[j])


plt.title(f"Gram matrix for {n} x {n} inputs of dim {d}")
plt.imshow(H)
plt.colorbar()

plt.show()

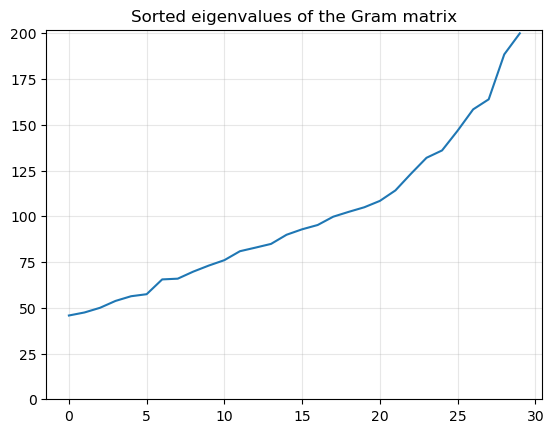
plt.title("Sorted eigenvalues of the Gram matrix")
eigvals = np.linalg.eigvalsh(H)
plt.plot(eigvals)
plt.grid(alpha=0.3)
plt.ylim(0, 1.01 * np.max(eigvals))
plt.show()

# mlp = MLPdeep() # MLPshallow()
# PATH = f'./{dataset.type}_{mlp.net_type}.pth'
# torch.save(mlp.state_dict(), PATH)

# net = MLPdeep() # MLPshallow()
# net.load_state_dict(torch.load(PATH))

Overparameterized linear regression

p = 1000
n = 100

X = np.random.normal(size=(p, n)) / np.sqrt(n)
Y = np.random.normal(size=(n, 1))

XXt = X @ X.transpose()
XY = X @ Y

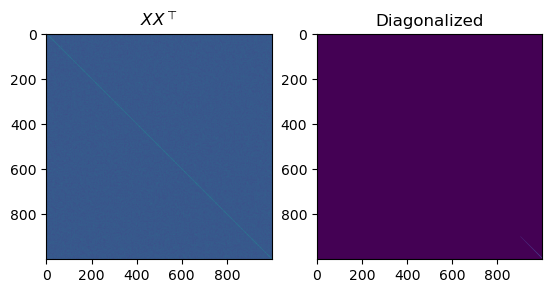
fig, axs = plt.subplots(1, 2)

axs[0].set_title(r"$X X^\top $")
axs[0].imshow(XXt)

eigvals, P = np.linalg.eigh(XXt)
print(rf"Largest eigenvalue of of XX^\top : {max(eigvals)}")

axs[1].set_title("Diagonalized")
axs[1].imshow(P.transpose() @ XXt @ P)
plt.show()

print(np.linalg.matrix_rank(X))

Largest eigenvalue of of XX^\top 16.963392764546683

100

T = 1000
eta = 0.001

ws = np.zeros((T, p, 1))
w = np.random.normal(size=(p, 1)) / np.sqrt(p)

losses = []
for t in range(T):
    w = w - eta * XXt @ w + eta * XY
    ws[t] = w

    losses.append(np.linalg.norm(X.transpose() @ w - Y) ** 2 / n)

ws = ws.squeeze(axis=2)
fig, axs = plt.subplots(1, 2, figsize=(16, 4))

axs[0].set_title("Loss")
axs[0].plot(losses)


axs[1].set_title("Relative distance of weights to init")
weight_evol = np.linalg.norm(ws - ws[0, :], axis=1) / np.linalg.norm(ws[0, :])
axs[1].plot(weight_evol, alpha=0.5)


plt.show()

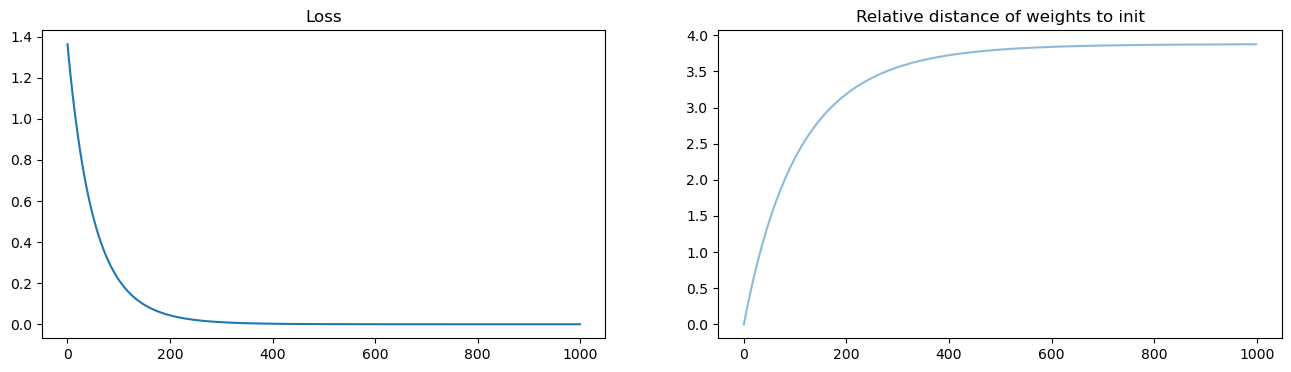
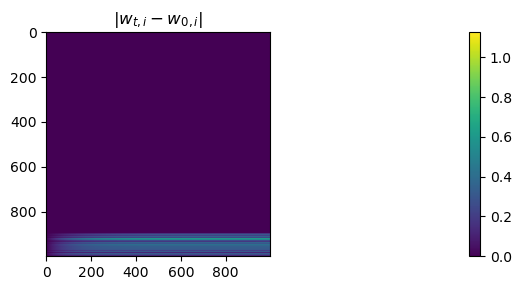
In the right basis, most coordinates of w dont move

w only moves in a low dimensional subspace: the image of X

fig, ax = plt.subplots(figsize=(40, 3))

plt.title(r"$|w_{t, i} - w_{0, i}|$")
ws_in_base = ws @ P

a = ax.imshow(np.abs((ws_in_base - ws_in_base[0]).transpose()))
fig.colorbar(a)
plt.tight_layout()
plt.show()